上回我們將使用者輸入的部分以及初始化的部分給完成了，這次接續將剩餘部分做完。將初始結點新增進open list之中，並確認初始結點是否為一個合法結點。若並非合法結點則直接輸入，讓使用者知道這種傳教士人數以及食人族人數的組合是沒有結果的。

 open_list.append(init)
    
# check whether the initial state is legal
if (not (state.isLegal((init), state.BoatState(1, 1, 0, 0)))):
    print("The condition doesn't have a solution.")
    sys.exit()

若通過上述的檢驗後，我們接續就要開始真正的結點展開了。我們只要當open list中還有結點並未展開或是我們展開的結點中遇到了終點的話，我們才會終止迴圈。每次的迴圈執行都是從open list中取出一個結點進行展開，展開後將此結點放進closed list之中，並將他所展開的所有結點放入open list之中。由於我們展開結點以及結點的合法性是分開處理的，因此我們先利用addChild函式獲得展開結點並暫存於一個list之中，接著遍歷list去確認結點是否合法，若合法才放進closed list之中。最後我們的open list還要根據f值以及h值的大小進行排序，如此才能保證取到終點時獲得的是最短路徑。
另外我們為了讓結果能夠呈現結點展開的用時為多久，我們在迴圈開頭以及結尾利用變數儲存了時間紀錄，以利到最後結果呈現的部分可以計算出耗時。(讀者可以自由選擇是否要加入)
設計如下：

timeStart = time.time()
while(len(open_list) != 0):
    current_state = open_list.pop(0)
    closed_list.append(current_state)
    if state.isGoal(current_state):
        result = True
        break

    children = []
    addChild(children, current_state)

    for child in children:
        if state.inOpen(child, open_list):
            for e in open_list:
                if e.m == child.m and e.c == child.c and e.a == child.a and e.b == child.b:
                    if child.g < e.g:
                        e = child
                    break
        else:
            open_list.append(child)

    # order open_list with the key: f(x) and cost(h(x) small and cost small -> forward)
    open_list = sorted(open_list, key = lambda x: x.h)
    open_list = sorted(open_list, key = lambda x: x.f)

timeEnd = time.time()

最後就是結果呈現的部分了，如果我們最後open list內所有結點都已經展開了卻還是沒有獲得終點的話，那麼便告訴使用者這樣的組合沒有結果。反之，將結果路徑以及用時給展示出來。
另外在展示結果時記得先將list給反轉，因為我們從closed list中獲得最短路徑時，是從終點到回去起點的，因此必須將結果給反轉，呈現出來的才會是起點至終點的路徑。

設計如下：

if result == True:
    print("-" * 50)
    print("Missionary Cannibal Boat_A Boat_B state")
    answer = state.showResult(closed_list)
    answer = reversed(answer)
    for e in answer:
        e.display()
    print("-" * 50)
    print("Total cost = ", closed_list[-1].g, ", total nodes = ", len(open_list) + len(closed_list))
    print("Time: ", str(round(timeEnd - timeStart, 2)), "sec")
else:
    print("The condition doesn't have a solution.")

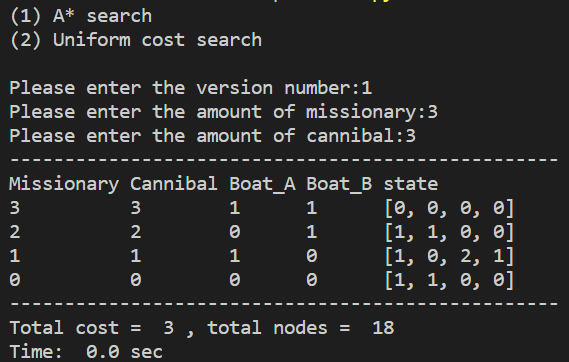
效果如下：